| Initiation aux probabilités Auteur : -Pika- Contributeur(s) : Cet article a pour but de faire une brève introduction aux probabilités générales en corrélation avec le Texas hold'em. D'autres articles suivront, notamment pour développer les probabilités cumulées, et d'établir un rapport entre les côtes et les probabilités. I. GénéralitésUn jeu de cartes contient 52 cartes différentes. Une main étant composée de deux de ces cartes, la probabilité d'avoir une main déterminée est de 52*51, soit 2652 mains. Néanmoins, l'ordre dans lequel les cartes sont distribuées n'ayant aucune importance, chaque main de départ est comptée deux fois (Exemple : la main   et la main et la main   sont au final une seule et même main dans ce jeu). Ce qui fait 2652/2 = 1326 mains de départ. sont au final une seule et même main dans ce jeu). Ce qui fait 2652/2 = 1326 mains de départ.II. Probabilités relatives aux différentes mains de départNous distinguerons ici les différentes catégories de mains : Les paires, les mains assorties, et les mains non-assorties qui ne sont pas des paires. A. Les pairesIl y a six "couples" différents de chaque paire. Prenons par exemple la paire d'as :   , ,   , ,  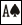 , ,   , ,  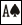 , ,  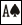 Il y a donc une chance sur 221 (1326/6) d'avoir une paire définie. Il y a treize paires différentes. Il y a donc une chance sur 17 (221/13) d'avoir une paire quelconque, soit 5.9%. B. Les mains assortiesIsolons une famille du jeu (par exemple les piques), et calculons le nombre de mains possibles : 12 mains composées d'un as, puis 11 composées d'un roi si l'on enlève 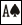 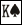 qui a déja été compté dans les 12 mains composées d'un as, et ainsi de suite. qui a déja été compté dans les 12 mains composées d'un as, et ainsi de suite. Il y a donc 12+11+10+9+8+7+6+5+4+3+2+1 = 78 mains différentes assorties à pique. Et par conséquent 312 (78*4) mains assorties au total, soit une chance sur 4.25 (1326/312), soit 23.5% des mains. Pour une main donnée, comme AK assorti, il y a donc une chance sur 331.5 (1326/4). C. Les mains non-assorties qui ne sont pas des pairesSimplifions le calcul. Nous avons vu que pour une famille donnée, il y a 78 mains différentes. Prenons une de ces mains, par exemple AK. Il y a 16 AK possibles :   , ,   , ,  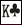 , ,  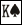 , ,   , ,   , ,  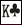 , ,  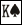 , ,   , ,   , ,  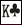 , ,  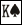 , , 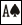  , , 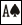  , , 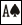 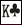 et et 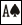 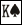 . .Sur ces 16 couples de mains, 4 sont assortis et 12 sont dépareillés. Il y a donc 3 fois plus de mains dépareillées qu'assorties, paires exclues. Nous avions calculé précédemment qu'il y a 312 mains assorties. Par conséquent, il y a 936 mains dépareillées, paires exclues. Nous avions également calculé qu'il y avait 1326 mains de départ possibles au texas hold'em. 78 paires + 312 mains assorties + 936 mains dépareillées qui ne sont pas des paires = 1326. Le compte est bon. D. Conclusion et remarquesL'importance des probabilités données ci-dessus ne saute pas aux yeux. Elles sont néanmoins la base même de calcul de toutes les autres probabilités, et sont par leur relative simplicité une bonne façon de s'initier aux probabilités. Dans le prochain article, nous aborderons les probabilités cumulées, la façon de calculer les outs et les côtes de pot. E. Entrainement1. Quelle probabilité ai-je d'avoir en main de départ ppT+, ATs+, AJo+ et KQs ? 2. Ai-je plus de chances d'avoir AQ+ (assorti ou non), ou bien d'avoir ppT+ ? sebreym (Jeudi 06 Août 2009 - 19:07) : Désolé d'avoir trainé pour valider ton article Pika ;) (Jeudi 06 Août 2009 - 21:54) : merci à toi de gérer ça, quel que soit le temps que tu mette à valider c'est déja honorable de s'en occuper : ) Et puis tout le monde est en vacances, ça change pas grand chose Pour ceux qui veulent proposer leurs solutions à la partie E. Entrainement, le mieux serait de passer par MP. Et vivement le dernier WE d'août chez Simon qu'on se fasse un live ça commence à me manquer grave là ! olivgoal (Mercredi 12 Août 2009 - 11:44) : J'ai lu l'article et j'aime bien ! Par contre ce qui m'intéresse plus c'est ce que je fais de la main que l'on me donne....la proba de recevoir une main ou une autre a la limite peu importe.... Je veux dire par la que : pendant le jeu, il y'a déjà tellement de choses a connaitre et a calculer que ces chiffres la sont un détail... par contre ils sont la base même du jeu, donc c'est toujours intéressant de les avoir vu au moins une fois et de comprendre comment les retrouver Kevin (Mercredi 12 Août 2009 - 12:51) : bon article, mais je suis d'accord avec olivgoal. c'est des probas pour un problème de maths : ca ne sert pas à grand chose en jeu. même dans un raisonnement "il est très peu probable qu'il ait reçu telle main" ca reste faux. (Vendredi 14 Août 2009 - 21:48) : Merci, le but est justement de pouvoir aborder avec de bonnes bases l'article 2, qui portera sur les probabilités cumulées, les cotes et les outs. Il devrait arriver bientôt, il est quasiment fini mais en stand-by depuis 3 semaines. J'essaie de faire ça ce week-end. davibaum (Vendredi 28 Août 2009 - 18:03) : c'est sur, cela ne sert pas a mieux jouer mes cela peut te permetre de savoir si tu suis quelle sont les chance que tu a par rapport a la mise ou a la relance que tu fait,et de voir si le risque que tu prend peut etre couvert par les maths.Mais tous cela mis a par il ne faut pas oublier le facteur chance Torrent007 (Jeudi 18 Avril 2013 - 12:27) : Up ! ;) |
|
Site CPPM v2 créé par lemonhead en Décembre 2005. Tous droits réservés.
Le site est optimisé pour une résolution de 1024x768 ou plus, et peut être correctement visualisé
avec Firefox 1.0+, Mozilla 1.3+, Opera 5.0+ ou à la limite, Internet Explorer 5.5+.
Si vous constatez un problème d'affichage, vous pouvez envoyer un mail au webmaster en précisant votre browser et sa version.
Webmaster : webmaster.cppm@club-poker-cppm.fr
Le site est optimisé pour une résolution de 1024x768 ou plus, et peut être correctement visualisé
avec Firefox 1.0+, Mozilla 1.3+, Opera 5.0+ ou à la limite, Internet Explorer 5.5+.
Si vous constatez un problème d'affichage, vous pouvez envoyer un mail au webmaster en précisant votre browser et sa version.
Webmaster : webmaster.cppm@club-poker-cppm.fr